Page 218 - 水土保持手冊_10612

3
3
2
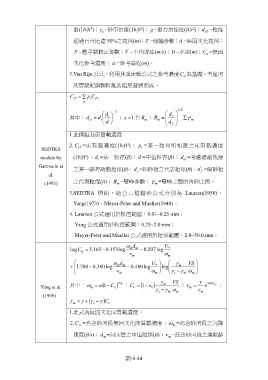
重(1b/ft )；γ =砂單位重(1b/ft )； g =重力加速度(ft/s )；d =粒徑
s
50
通過百分比達 50%之粒徑(m)；T =傳輸參數；d =無因次化粒徑；
F =懸浮載修正係數；V =平均流速(m/s)；D =水深(m)；C =無因
a
次化參考濃度；α =參考高程(m)。

3.Van Rijn 公式，利用其溪床載公式之參考濃度C 為基礎，考慮河
a
床質級配與顆粒亂流阻尼發展而成。

C t* = ∑ Cp i t* i
k

x
−

i
=
其中： d = d i  d   ； x 1 / 7 . B ； B m =   d c   2 / 1 ∑ p
m
m
ei
 d    d f  
1.此模組為床質載濃度
3
2. C =床質載濃度(1b/ft )； p =某一粒徑所相應之床質載濃度
SEDTRA * t i
3
module by (1b/ft )； d =某一粒徑(ft)； d =中值粒徑(ft)； d =考慮遮蔽效應
i
ei
Garbrecht et
之某一臨界啟動粒徑(ft)；d =粗砂粒之代表粒徑(ft)；d =細砂粒
f
c
al.
(1995) 之代表粒徑(ft)； B =雙峰參數； p =雙峰之間的含砂比例。
m
m
3.SEDTRA 模組，結合三種輸砂公式分別為 Laursen(1958)、
Yang(1973)、Meyer-Peter and Mueller(1948)。
4. Laursen 公式適用於粒徑範圍：0.01~0.25 mm；

Yang 公式適用於粒徑範圍：0.25~2.0 mm；

Meyer-Peter and Mueller 公式適用於粒徑範圍：2.0~50.0 mm。

ω d U
log C = 165.5 − 153.0 log m m − 297.0 log *
ts
v m ω m
 ω d U   γ VS 
+  780.1 − 360.0 log m m − 480.0 log * log  m 




 v m ω m   γ s −γ m ω m 
γ
γ
0 . 7
( −
Yang et al. 其中：ω m = ω (1 C− v ) ； C = 1 e b ) γ − m γ VS ； v = γ e 506 C v ；
v
m
ω
(1996) s m m m
γ = γ + (γ − γ )C
m
v
s
1.此式為無因次化床質載濃度。
2.C =高含砂河段無因次化床質載濃度；ω =高含砂河段之沉降
m
ts
速度(ft/s)；d =河床質之中值粒徑(ft)；ν =高含砂河段之運動黏
m
m

調-4-44